卷积神经网络
6.卷积神经网络
1.卷积神经网络的优势
1.1 平移不变性
卷积核不依赖于当前图片的位置$(i,j)$ ,仅取决于自己,具有平移不变性。
平移不变性:卷积过程中卷积核不变,共享同一组权重。
1.2 局部性
卷积运算仅取决于当时的图像位置(卷积核大小),具有局部性。
局部性:指不考虑整个图像,仅计算当前的窗口,这个窗口有个官方名字叫感受野。
2.卷积层具体含义
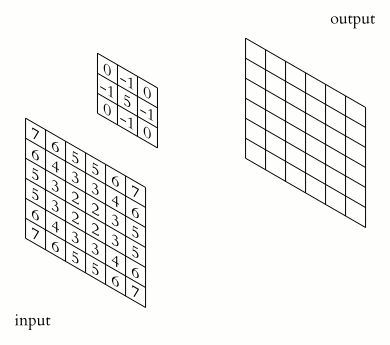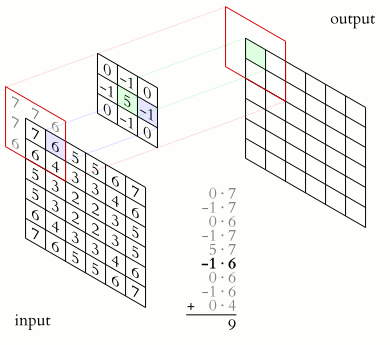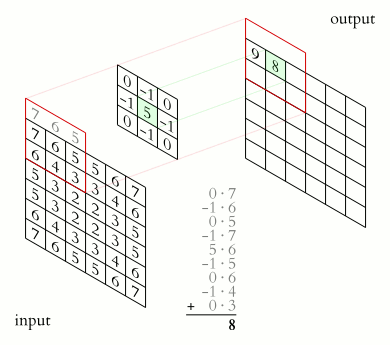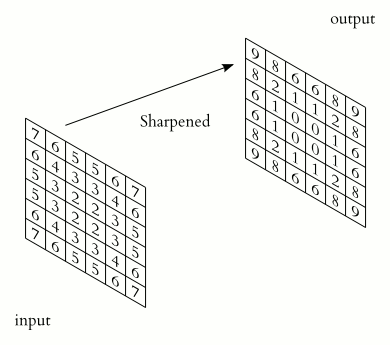
卷积层就是一个特殊的全连接层:对全连接层使用平移不变性和局部性得到卷积层。

$$
输入\mathbf X:n_h\times n_w\
核\mathbf W:k_h\times k_w\
偏差b\in \mathbb R\
输出\mathbf Y:(n_h-k_h+1)\times (n_w-k_w+1)\
\mathbf Y=\mathbf X\star \mathbf W+b
$$
如上述公式所示:卷积层将输入$\mathbf X$和核矩阵$\mathbf W$进行交叉相关(卷积),加上偏移$b$后得到输出。
注意:核矩阵$\mathbf W$和偏移$b$都是可以学习的参数,核矩阵的大小是超参数。
3.填充与步幅
填充和步幅是卷积层的超参数。
- 填充(Padding):
- 目的:在输入特征图的边缘添加额外的行和列(通常是0),以控制输出特征图的空间尺寸,通常是控制输出形状的减少量。
- 为什么需要它:
- 保持尺寸:使输出特征图与输入特征图的高度和宽度相同。
- 防止边缘信息丢失:避免图像边缘的像素在卷积过程中被“忽略”太多次。
- 步幅(Stride):
- 目的:每次滑动核窗口时的行/列的步长,可以成倍的减少输出形状。
- 为什么需要它:
- 降维:快速减小输出特征图的尺寸,减少计算量和参数。
- 扩大感受野:更大的步幅使得输出中的一个像素对应输入中更大范围的区域。
输出特征图的尺寸由以下通用公式决定:
$$
Y_h=\lfloor \frac{X_h-K_h+P_u+P_b}{S_h} \rfloor+1\
Y_w=\lfloor \frac{X_w-K_w+P_l+P_r}{S_w} \rfloor+1
$$
其中,
输出高度 = ⌊(输入高度 - 卷积核高度 + 填充高度上 + 填充高度下) / 步幅高度⌋ + 1;
输出宽度 = ⌊(输入宽度 - 卷积核宽度 + 填充宽度左 + 填充宽度右) / 步幅宽度⌋ + 1。
当填充是对称的,步幅相等,并且输入是正方形,卷积核也是正方形时,公式简化为:
$$
\frac{(X-K+2P)}{S}+1
$$
4.输入通道数和输出通道数
输入通道数:
- 第一层:由数据决定(彩色图=3,黑白图=1)
- 后面层:由前一层的输出通道数决定
输出通道数:
- 是可以调节的超参数
- 通常越深的层,通道数越多
- 更多的通道 = 更丰富的特征表示能力
卷积核通道数等于输入通道数,卷积核数等于输出通道数。
$$
输入\mathbf X:c_i\times n_h\times n_w\
核\mathbf W:c_o\times c_i\times k_h\times k_w\
输出\mathbf Y:c_o\times m_h\times m_w
$$
每个输入通道有独立的二维卷积核,所有通道结果相加得到一个输出通道结果。
每个输出通道有独立的三维卷积核,每个核生成一个输出通道。
输出通道数也是卷积层的超参数。
5.池化层
5.1 引入原因
卷积层对位置过于敏感,而池化层具有一定程度的容忍性,可以用来缓解卷积层对位置的敏感度。
🎯 用一个超简单的比喻
想象一下:卷积层是个「强迫症侦探」,池化层是个「粗心大意的主管」。
侦探 vs 主管的工作方式:
卷积层(强迫症侦探):
- “报告!我在照片的第125行第87列发现了一个眼睛!”
- “注意!这次眼睛在第126行第88列,位置变了!”
- 对每个像素的位置都斤斤计较。
池化层(粗心主管):
- “我不管眼睛在左上角还是右下角…”
- “我只关心:这张图里到底有没有眼睛?”
- “把最重要的特征告诉我,具体位置我不在乎!”
5.2 最大池化层和平均池化层
🎯 池化层 = 「固定规则的过滤器」
池化层与卷积层类似,都具有填充和步幅;且只有两种固定的池化规则,因此没有可学习的参数。
最大池化层:选取每个窗口中最强的模式信号。
平均池化层:将最大池化层中的“最大”操作替换为“平均”。
🎯 池化层 = 「平行处理的流水线」
在每个输入通道应用池化层以获得相应的输出通道,虽然池化层的操作相同,但是处理的内容不同,就像并行的流水线一样。并不改变输出的通道数,也就是输出的通道数=输入的通道数。


